236. 二叉树的最近公共祖先

Similar Question

leading to the advanced question

Solution Tips

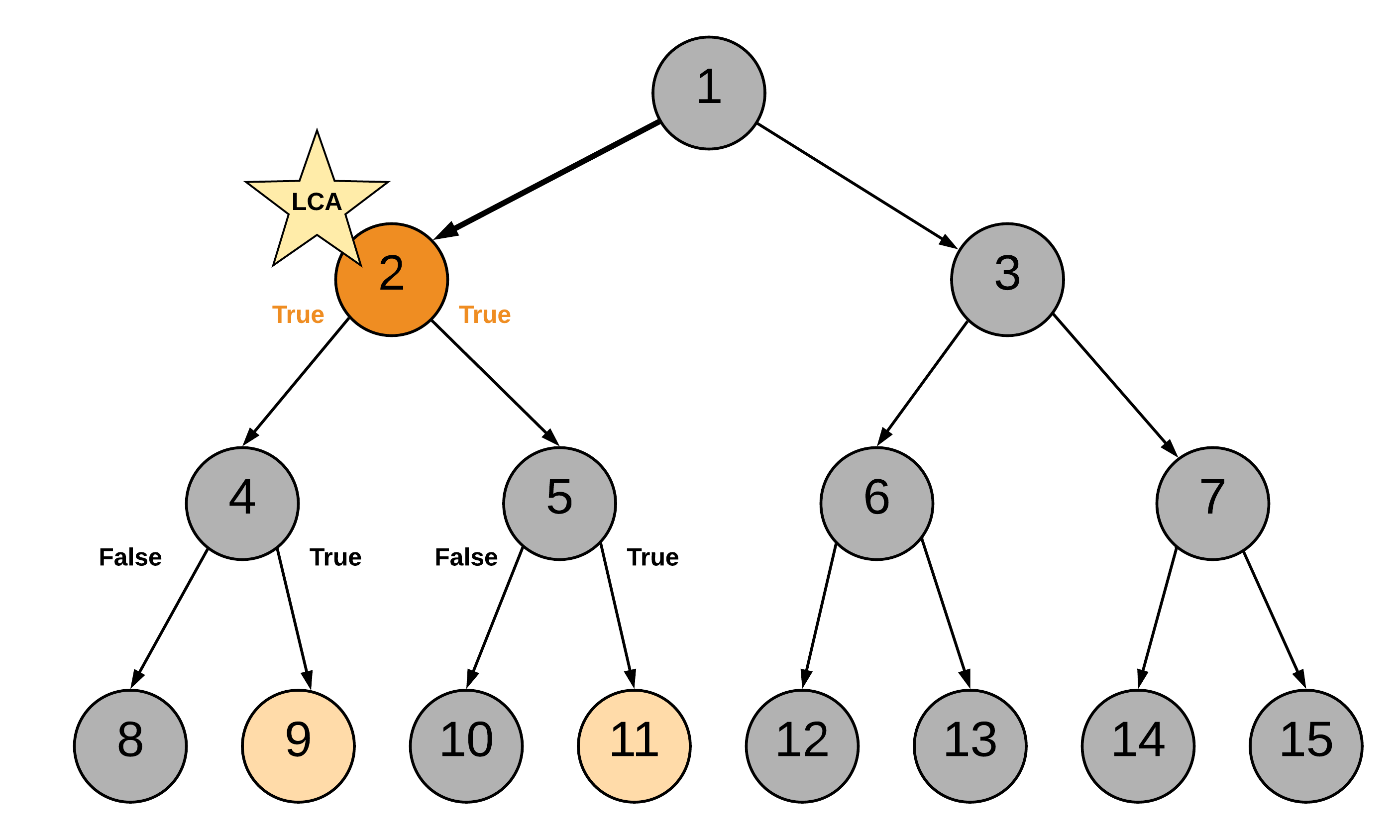
方案一: 一左一右

这种方法非常直观。先深度遍历改树。当你遇到节点 p 或 q 时，返回一些布尔标记。该标志有助于确定是否在任何路径中找到了所需的节点。在子树的递归中，如果该子树找到了目标节点，就标记为真

算法：

1. 从根节点开始遍历树。
2. 如果当前节点本身是 p 或 q 中的一个，我们会将变量 mid 标记为 true，并继续搜索左右分支中的另一个节点。
3. 如果左分支或右分支中的任何一个返回 true，则表示在下面找到了两个节点中的一个。
4. 如果在遍历的任何点上，左、右或中三个标志中的任意两个变为 true，这意味着我们找到了节点 p 和 q 的最近公共祖先。

  const {BST} = require('./utils/structure/BST')
  const bst = new BST()
  let p = bst.insert(1)
  bst.insert(2)
  let q = bst.insert(3)
  bst.insert(4)
  bst.insert(5)
  bst.insert(6)
  bst.insert(7)
  
  var lowestCommonAncestor = function(root, p, q) {
    let res = null
    recursion(root,p,q)
    return res
    function recursion(root,p,q){
      if(root===null) return false
  
      let mid= (root===p || root === q)? 1 : 0
      let left = recursion(root.left,p,q)? 1 : 0
      let right = recursion(root.right,p,q)? 1 : 0
    
      if(mid + left + right >= 2) res = root
      return mid + left + right > 0
    }
  }
  
  console.log(lowestCommonAncestor(bst.root(),p,q))

问题在于已经找到了最近的公共祖先之后，还有很多多余的遍历，无法中断遍历

方案二: 迭代

在前面的方法中，我们在回溯过程中遇到 LCA。我们可以摆脱回溯过程本身。在这种方法中，我们总是有一个指向可能 LCA 的指针，当我们找到两个节点时，我们返回指针作为答案。

算法：

1. 从根节点开始。
2. 将 (root, root_state) 放在堆栈上。root_state 定义要遍历该节点的一个子节点还是两个子节点。
3. 当堆栈不为空时，查看堆栈的顶部元素，该元素表示为 (parent_node, parent_state)。
4. 在遍历 parent_node 的任何子节点之前，我们检查 parent_node 本身是否是 p 或 q 中的一个。
5. 当我们第一次找到 p 或 q 的时候，设置一个布尔标记，名为 one_node_found 为 true 。还可以通过在变量 LCA_index 中记录堆栈的顶部索引来跟踪最近的公共祖先。因为堆栈的所有当前元素都是我们刚刚发现的节点的祖先。
6. 第二次 parent_node == p or parent_node == q 意味着我们找到了两个节点，我们可以返回 LCA node。
7. 每当我们访问 parent_node 的子节点时，我们将 (parent_node, updated_parent_state) 推到堆栈上。我们更新父级的状态为子级/分支已被访问/处理，并且相应地更改状态。
8. 当状态变为 BOTH_DONE 时，最终会从堆栈中弹出一个节点，这意味着左、右子树都被推到堆栈上并进行处理。
9. 如果 one_node_found 是 true 的，那么我们需要检查被弹出的顶部节点是否可能是找到的节点的祖先之一。
10. 在这种情况下，我们需要将 LCA_index 减少一个。因为其中一位祖先被弹出了。 当同时找到 p 和 q 时，LCA_index 将指向堆栈中包含 p 和 q 之间所有公共祖先的索引。并且 LCA_index 元素具有 p 和 q 之间的最近公共祖先。

  import javafx.util.*;
  
  class Solution {
  
    // Three static flags to keep track of post-order traversal.
  
    // Both left and right traversal pending for a node.
    // Indicates the nodes children are yet to be traversed.
    private static int BOTH_PENDING = 2;
  
    // Left traversal done.
    private static int LEFT_DONE = 1;
  
    // Both left and right traversal done for a node.
    // Indicates the node can be popped off the stack.
    private static int BOTH_DONE = 0;
  
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  
      Stack<Pair<TreeNode, Integer>> stack = new Stack<Pair<TreeNode, Integer>>();
  
      // Initialize the stack with the root node.
      stack.push(new Pair<TreeNode, Integer>(root, Solution.BOTH_PENDING));
  
      // This flag is set when either one of p or q is found.
      boolean one_node_found = false;
  
      // This is used to keep track of the LCA.
      TreeNode LCA = null;
  
      // Child node
      TreeNode child_node = null;
  
      // We do a post order traversal of the binary tree using stack
      while (!stack.isEmpty()) {
  
        Pair<TreeNode, Integer> top = stack.peek();
        TreeNode parent_node = top.getKey();
        int parent_state = top.getValue();
  
        // If the parent_state is not equal to BOTH_DONE,
        // this means the parent_node can't be popped off yet.
        if (parent_state != Solution.BOTH_DONE) {
  
          // If both child traversals are pending
          if (parent_state == Solution.BOTH_PENDING) {
  
            // Check if the current parent_node is either p or q.
            if (parent_node == p || parent_node == q) {
  
              // If one_node_found was set already, this means we have found
              // both the nodes.
              if (one_node_found) {
                return LCA;
              } else {
                // Otherwise, set one_node_found to True,
                // to mark one of p and q is found.
                one_node_found = true;
  
                // Save the current top element of stack as the LCA.
                LCA = stack.peek().getKey();
              }
            }
  
            // If both pending, traverse the left child first
            child_node = parent_node.left;
          } else {
            // traverse right child
            child_node = parent_node.right;
          }
  
          // Update the node state at the top of the stack
          // Since we have visited one more child.
          stack.pop();
          stack.push(new Pair<TreeNode, Integer>(parent_node, parent_state - 1));
  
          // Add the child node to the stack for traversal.
          if (child_node != null) {
            stack.push(new Pair<TreeNode, Integer>(child_node, Solution.BOTH_PENDING));
          }
        } else {
  
          // If the parent_state of the node is both done,
          // the top node could be popped off the stack.
          // Update the LCA node to be the next top node.
          if (LCA == stack.pop().getKey() && one_node_found) {
            LCA = stack.peek().getKey();
          }
  
        }
      }
      return null;
    }
  }

var lowestCommonAncestor = function(root, p, q) {
  const BOTH_PENDING = 2,
        LEFT_DONE = 1,
        BOTH_DONE = 0
  const stack = new Stack()
  // Initialize the stack with the root node.
  stack.push([root,BOTH_PENDING])
  let oneNodeFound = false, // This flag is set when either one of p or q is found.
      LCA = null, // This is used to keep track of the LCA.
      childNode = null
  // We do a post order traversal of the binary tree using stack
  while(!stack.isEmpty()){
    const top = stack.pop()
    const parentNode = top[0],
          parentState = top[1]
  }
}